The Geometer

There’s a course about computational geometry which I scripted from the source in maXbox. The origin you can find at:

http://www.delphiforfun.org/programs/Library/geometry1.htm

The script with the 9 Tasks in one file you can find at:

http://www.softwareschule.ch/examples/geometry.txt

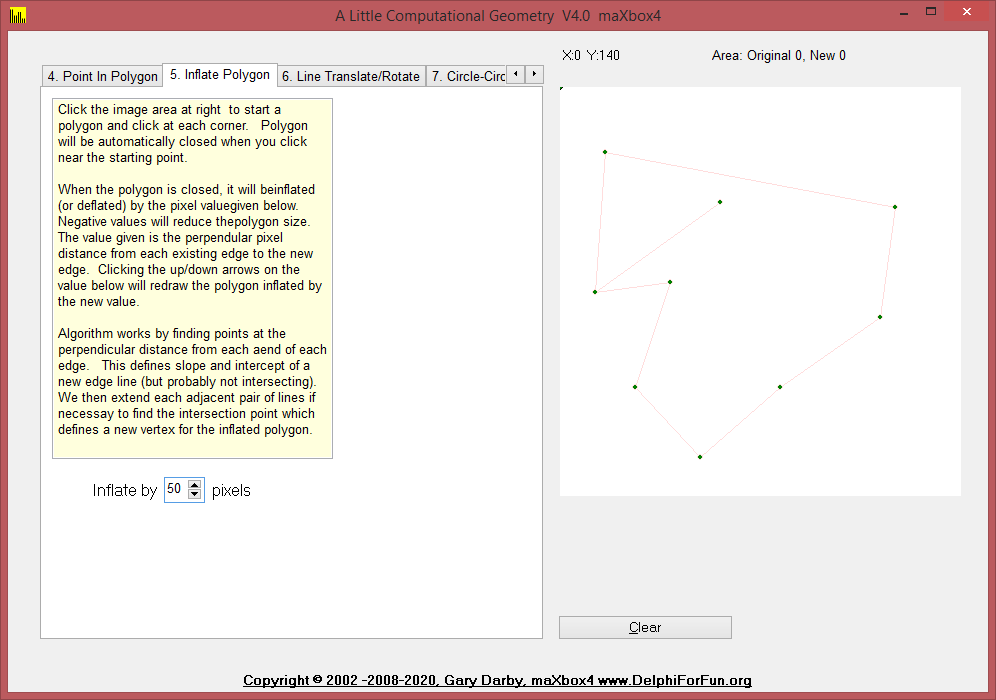
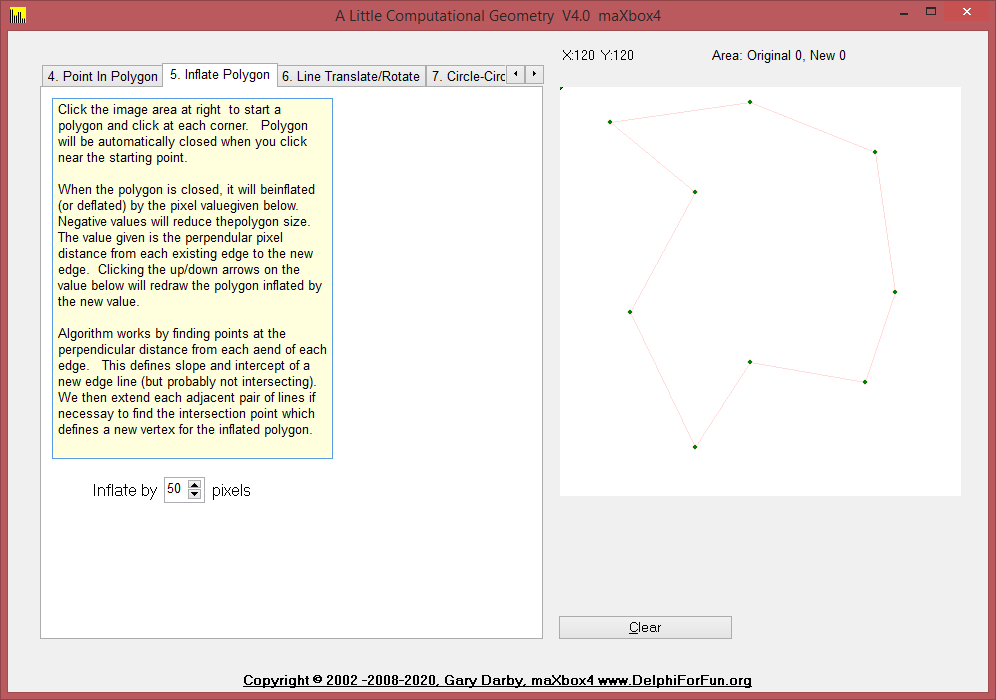
Three new routines were added to the UGeometry unit today and Version 3 of the  Geometry test program  illustrates their use.  The routines, PolygonArea, InflatePolygon, and PolygonClockwise help to “inflate” (or deflate) a given polygon by  given amount.  The value is the distance which the edges are to be moved while retaining their slope.

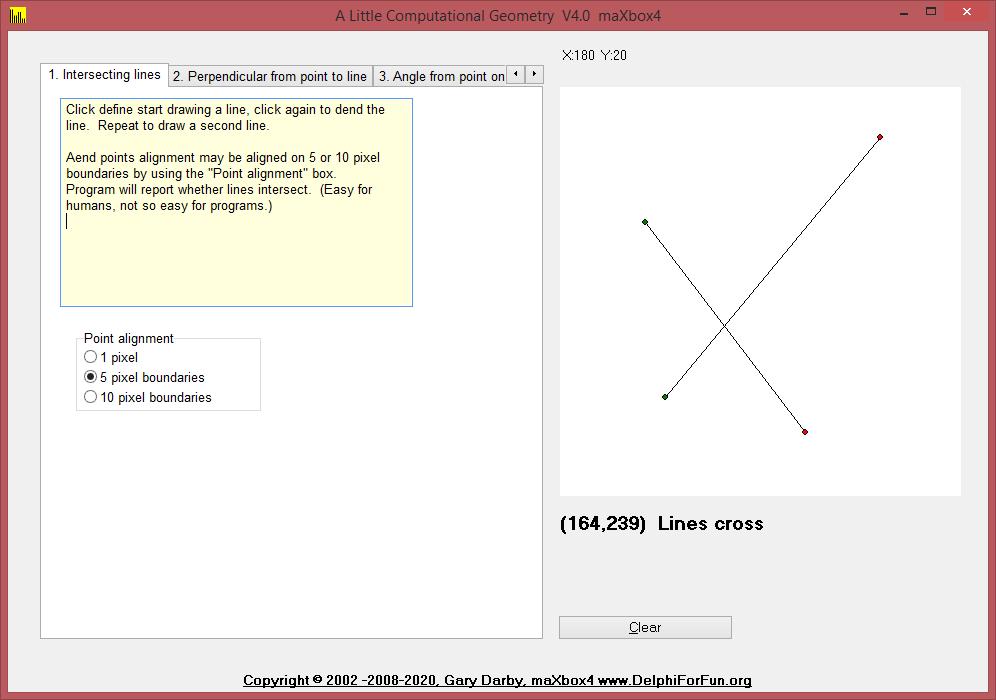
But we start from the beginning. 1. Intersect takes two line definitions as input and returns true if the two line intersect.  An additional parameter, PointOnBorder, is set to true if the lines touch but do not cross, .   This is a faster, but harder-to-understand  version of the IntersectingLines routine presented earlier.

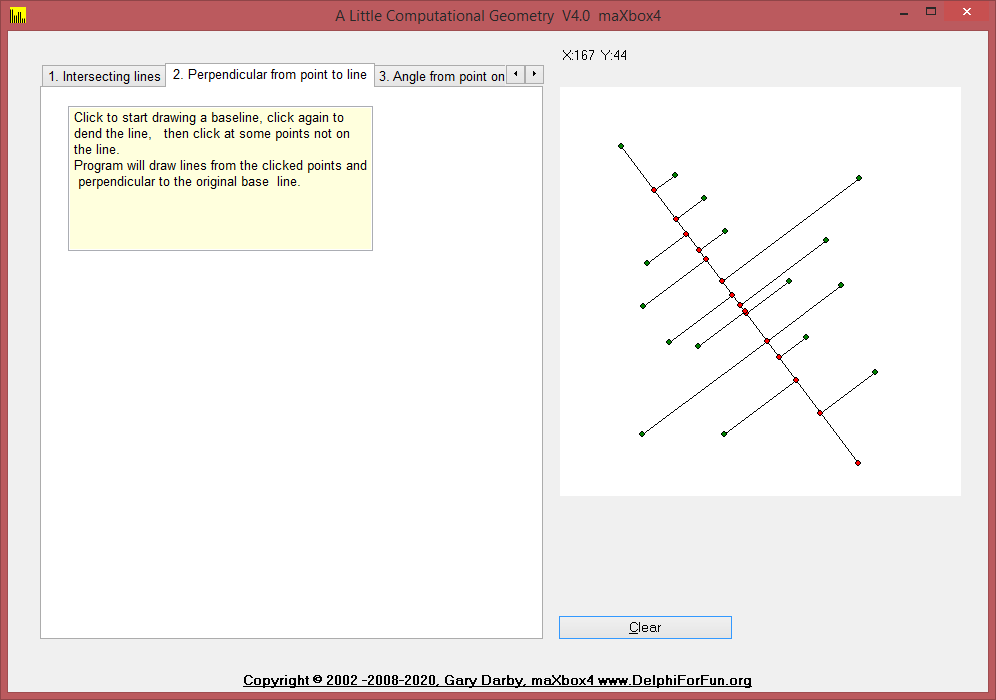
2. PointPerpendicularLine

Given a line and a point not on the line, construct a line through the point and perpendicular to the line.   The trick here is to determine the slope of the given line,  m, and take advantage of the fact that the slope of  a perpendicular line is -1/m.  Given the equations of the two lines we can solve them as decribed in Intersecting Lines to determine the point of intersection.  

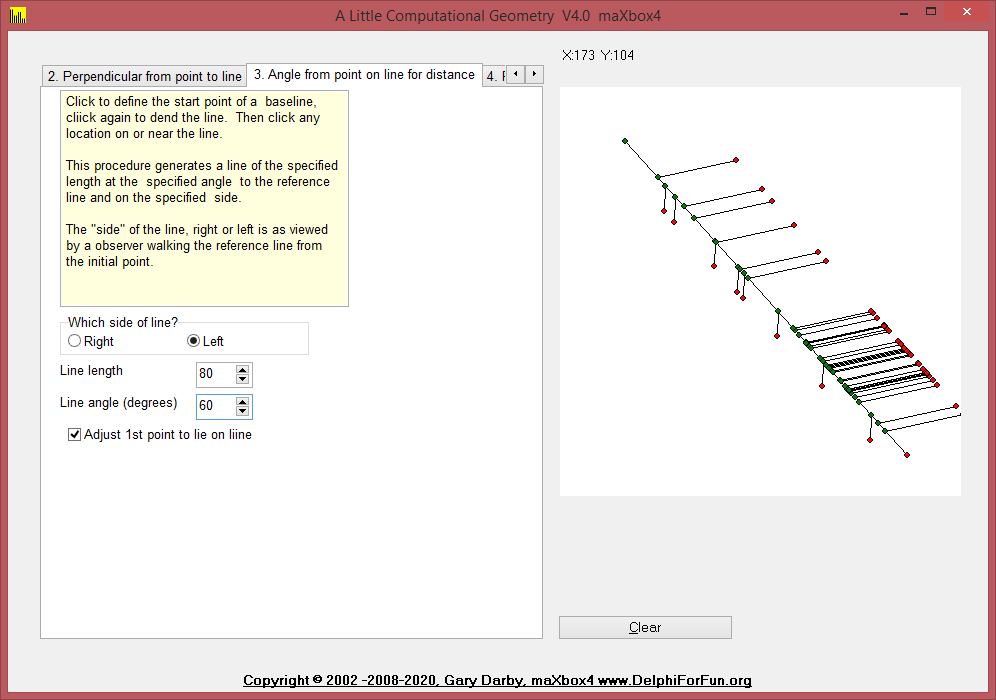
3. AngledLineFromLine

Given a line, a point on (or near) the line, an angle, and a length, construct a line through the point with the specified length and at the specified angle from the given line.   The simplest approach to this problem is to draw a line segment of a given length, L, at a given angle, A, through a given point, P.   The new point is defined by P2.X=P1.X+Lcos(A) and P2.Y=P1.Y+Lsin(A).  The only problem remaining is to determine angle A.  The required angle equals the angle of the given line from the horizon   plus the given angle, and the angle of the given line from the horizon is given by the inverse tangent of its slope.  Here’s the bit of Delphi code that does that for line L1 with endpoints p1 and p2:

else if pagecontrol1.activepage=AngleSheet then begin
    if dragval=2 then dragval:=3 {end of initial base line}
    else if dragval=3 then begin
      l2.p1:=point(x,y); 
{assume user wants the angle start point to be mouseup point}
      a:=angleEdt.value/180*Pi; 
{default, increase angle (counter clockwise)}
      if rightleftbox.itemindex=0 then a:=-a;  {right reduces angle}
      if adjustbox.checked then begin {drop perp from pt to line first}
        L2:=pointperpendicularLine(L1,L2.p1);
        l2.p1:=l2.p2; {and make that the new line start point}
      end;
      L2:=AngledLineFromLine(L1,L2.P1,distedt.value,a);
      drawline(l2);
    end;

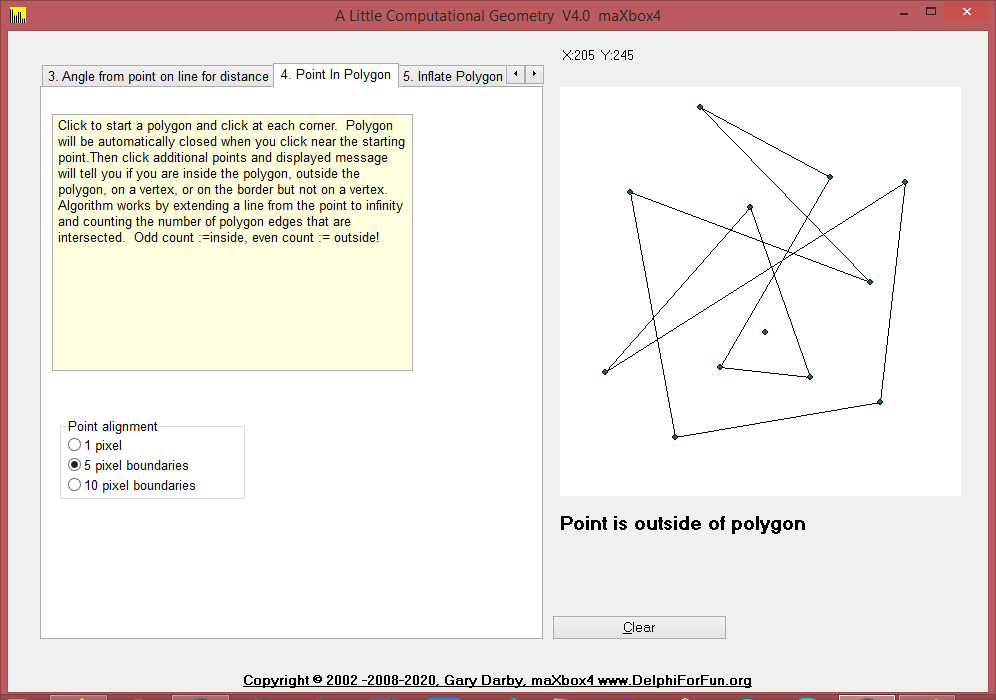
4. Point In Polygon

Given an arbitrary polygon and a point, determine if the point is inside or outside of the polygon.  (The red point in the image at left is outside of the polygon.)

The algorithm extends a line from the point to “infinity: and counts how many times it intersects the polygon.  If odd, the point is internal; if even, the point is external to the polygon.   There are a few messy details here in detecting cases where the point is on an edge  or vertex of the polygon or when the extension line passes through a vertex.

5. InflatePolygon, and PolygonClockwise help to “inflate” (or deflate) a given polygon by  given amount.  The value is the distance which the edges are to be moved while retaining their slope.  In order to decide which direction to move each edge, we need to know whether the polygon was built in a clockwise or counterclockwise direction.

6. Translate / Rotate: These routines to translate and rotates lines are required for the Circle-Circle intersection operations.

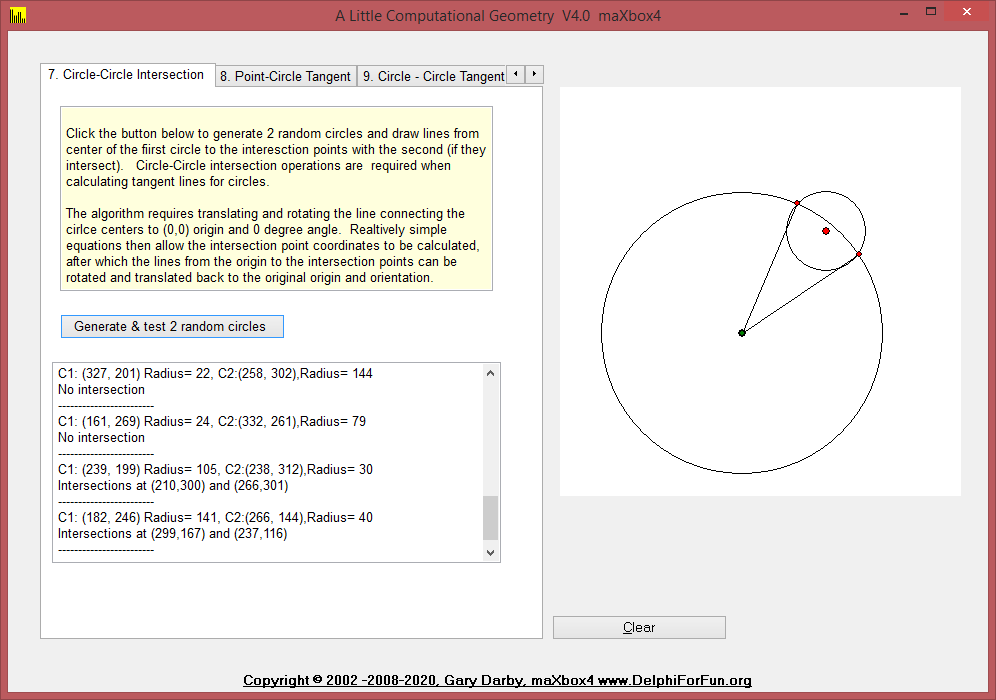
7. CircleCircleIntersect function to return the intersection points of 2 passed circles and CircleCircleExtTangentLines function calculates the 2 exterior tangent lines, if they exist, between 2 given circles.

if pagecontrol1.activepage=IntersectSheet then begin
        label2.caption:='X:'+inttostr(p.x)+'  Y:'+inttostr(p.y);
        if (dragval>0) and (not moved) then 
{first time just draw the start point}
        begin
          drawpoint(startpoint,pointcolor);
          moved:=true;
        end;
        case dragval of
          1:L1.p2:=point(x,y);
          3:L2.p2:=point(x,y);
        end;
        If dragval>0 then drawintersecting;
      end;

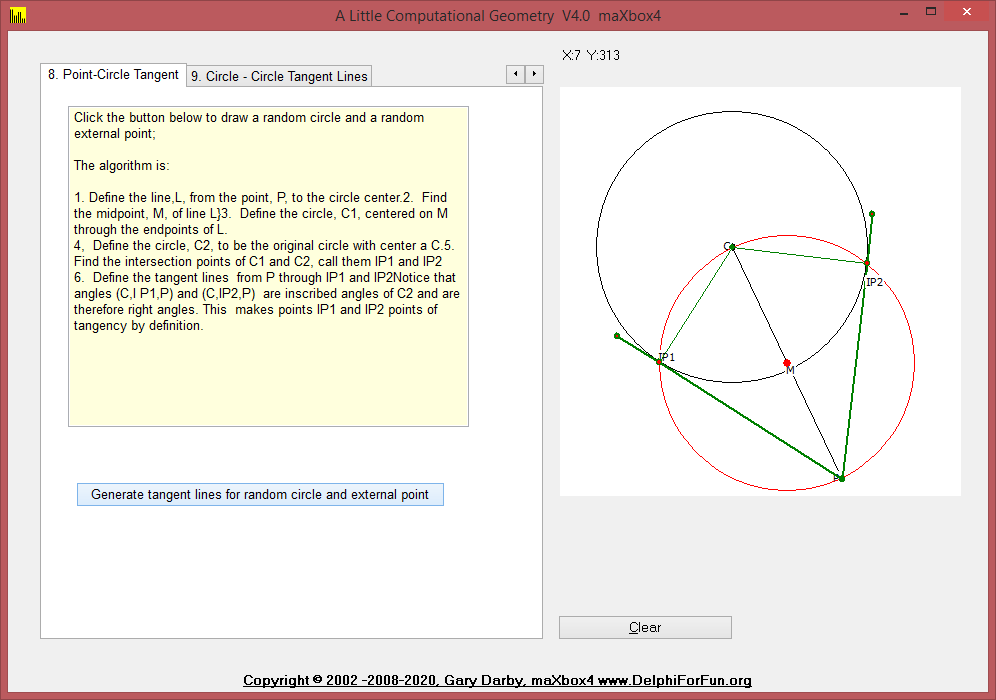
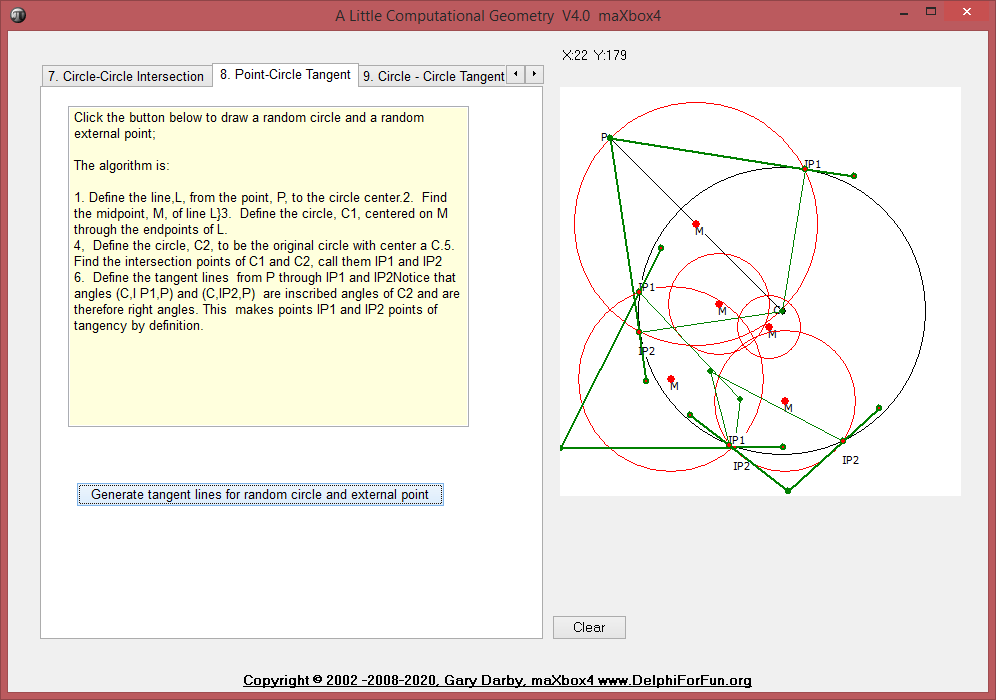
8. PointCircleTangentLines function calculates the two tangent lines to a given circle from a given exterior point.

else if pagecontrol1.activepage=TangentPC then begin
    if working <> anone then
    with circles[workingon] do begin
      erasecircle(circles[workingon]);
      if working=sizing then r:=intdist(point(cx,cy),point(x,y))
      else begin
        cx:=x;
        cy:=y;
      end;
      drawcircle(circles[workingon],clBlack);
    end;
  end;

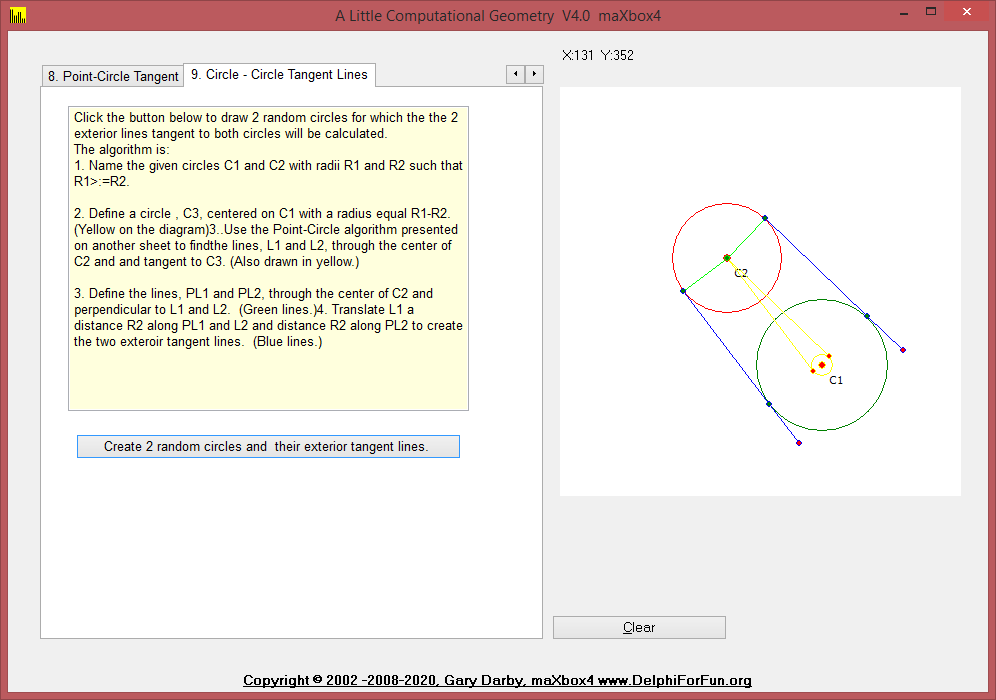
9. CircleCircleExtTangentLines function calculates the 2 exterior tangent lines, if they exist, between 2 given circles.

Click the button below to draw 2 random circles for which the the 2 exterior lines tangent to both circles will be calculated.
The algorithm is:

1. Name the given circles C1 and C2 with radii R1 and R2 such that R1>:=R2.

{*************** CircCircTanBtnClick *****************}
procedure CircCircTanBtnClick(Sender: TObject);
{Draw two random circles and their exterior tangents}

(*  procedure screenDrawLine(L:TLine);
  {Invert Y axis values for drawing on screen}
  begin
    with L do drawline(line(point(p1.x,-p1.y),point(p2.x,-p2.y)));
  end;    *)
var
  c1,c2,c3:TCircle;
  pc:TPoint;
  d:extended;
  L1,L2,Pl1,Pl2,TL1,TL2, extline:TLine;
  loops:integer;
begin
  reset;
  with c1, image1 do repeat
    cx:= random(width div 2)+ width div 3;
    cy:= random(width div 2)+ width div 3;
    r:=random(width div 3) + 20;
    pc:=point(cx,cy);
    with c2 do begin
      loops:=0;
      repeat
        cx:= random(width div 2)+ width div 3;
        cy:= random(width div 2)+ width div 3;
        r:=random(width div 3) + 20;
        d:=intdist(point(cx,cy),pc);
        inc(loops);
      until (d>c2.r+c1.r) or (loops>100);
    end;
  until d>c1.r+c2.r;

Der Kronometer

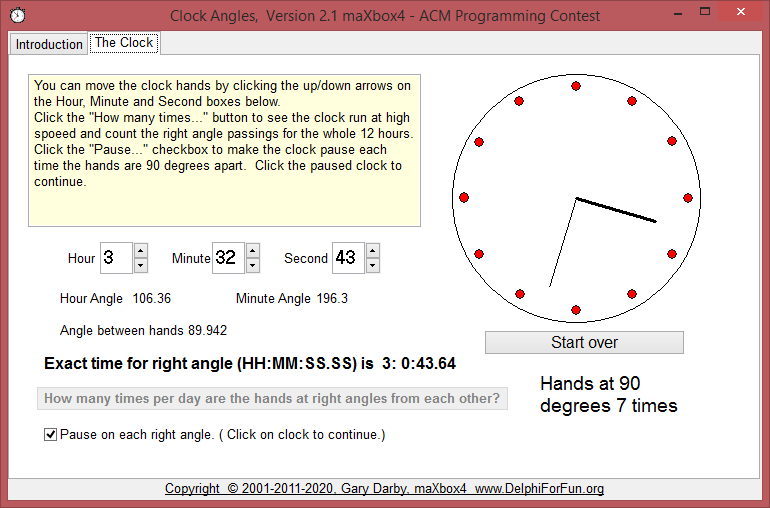
Here’s a beginner’s program that was adapted from an ACM Programming Contest.   Given  integers representing  hour and minute of a time of day, calculate the angle between the hour and minute hands when looking at a normal analog clock.

First the “computing the angles” part.   The angle of the minute hand  should be “# of degrees for each minute” X “# of minutes”.   Since 60 minutes represents 360 degrees, each minute represents 360/60 or  6 degrees.   (So 30 minutes becomes  6*30 = 180 degrees, etc.).   The hour hand is similar with one exception – the hour hand includes hours and and fractions of an hour (reflected by minutes) in its angle. 

http://www.softwareschule.ch/examples/time.txt

So the hour-time  is  “hours +  minutes/60”.  (  Hour-time for 6:30, for example, is 6+30/60 or 6.5).  Since the hour hand revolves 1/12 of a revolution or 30 degrees for each hour, the hour hand angle is 30 X  hour time.   If the time is 6:30, the hour hand angle is 30 X 6.5 = 195 degrees.   Finally, the angle difference between the hands is 195-180=15 degrees.

procedure ComputeAngles;
var
  hour,minute,second:integer;
  hourtime,minutetime:single;
begin
  hour:=hourval.position mod 12;
  minute:=minuteval.position;
  second:=secval.Position;
  hourtime:=(hour+minute/60+second/3600)/12;
  hourangle:=hourtime*360;
  minutetime:=minute/60+second/3600;
  minuteangle:=minutetime*360;
  difangle:=(minuteangle-hourangle);
  if difangle>180 then difangle:=difangle-360;
  if difangle<= -180 then difangle:=difangle+360;
  lha.caption:=floattostrf(hourangle,ffgeneral,5,2);
  lma.caption:=floattostrf(minuteangle,ffgeneral,5,2);
  lda.caption:=floattostrf(difangle,ffgeneral,5,2);
end;

Given a positive decimal  number, convert it to an irreducible mixed or  proper fraction.  If the denominator of the fraction is larger than a specified maximum denominator, present the solution in the above format as a fraction which is the best estimate of the input value and display the error value.  

http://www.delphiforfun.org/programs/Math_Topics/DecToFraction.htm

Version 3 – convert both ways (decimal to fraction, and fraction to decimal) and add optional constraint to display decimal input in mixed fraction form with  denominators restricted to 16, 32, or 64.

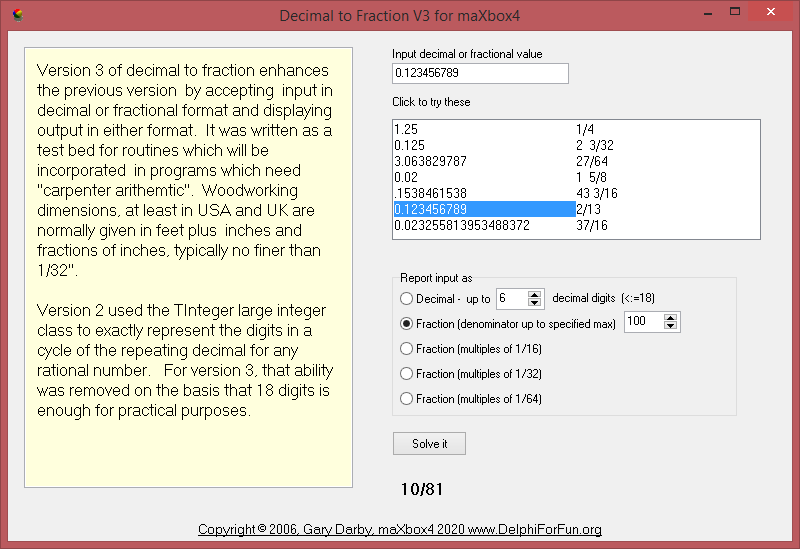
Otherwise, we’ll have to provide the closest possible estimate whose denominator is smaller than the maximum specified. We’ll just try all denominators from 2 to the max specified and calculate the numerator which produce a value closest to the original decimal part. Numerator = ((original decimal part) x trial denominator) rounded to the nearest integer.