MIDI Magic

Posted bymaxbox4Posted inCode, maXbox, SynthesizerTags:, , , ,

The General MIDI specification defines 128 instruments, and 47 percussion sounds. All channels except channel 9 (counting from zero) play instruments, channel 9 plays percussion sounds, with different note numbers resulting in different sounds. The MIDI standard itself does not define any instruments or percussion sounds.

Other specifications (General MIDI 2, GS, XG etc.) define more sounds, and have mechanisms to select which channel(s) to use for percussion sounds.

So first we set our Midi Controller or Device:

var note: TMidinote;
    tmidi: TJclMIDIOut;
    fMidiOut: IJclMidiOut;
    fChannel: TMidiChannel;

mlist:= THashedStringList.create;
   GetMidiOutputs(mlist);  //check for midi devices
   writeln(mlist.text)
   mlist.free;
fmidiout:= MIDIOut(0);
//fmidiout.SendMessage(const Data: array of Byte);
fmidiout.SwitchPolyModeOn(16);
writ(fmidiout.getname);
fmidiout.SendNoteOn(2, note+36, $7f); //test tone

So we set an interface from IJclMidiOut and we get an instance of JclWinMIDI.MIDIOut(DeviceID); 

type
  TJclWinMidiOut = class(TJclMidiOut, IJclWinMidiOut)
function MidiOut(DeviceID: Cardinal): IJclWinMidiOut;
procedure GetMidiOutputs(const List: TStrings);
procedure MidiOutCheck(Code: MMResult);

We can see our device as Microsoft GS Wavetable Synth

Next we play a tune:

playTune(['g4','g#4','a#4','c5','d5','d#5','f5','g5'], 500, 4, true, fmidiout);
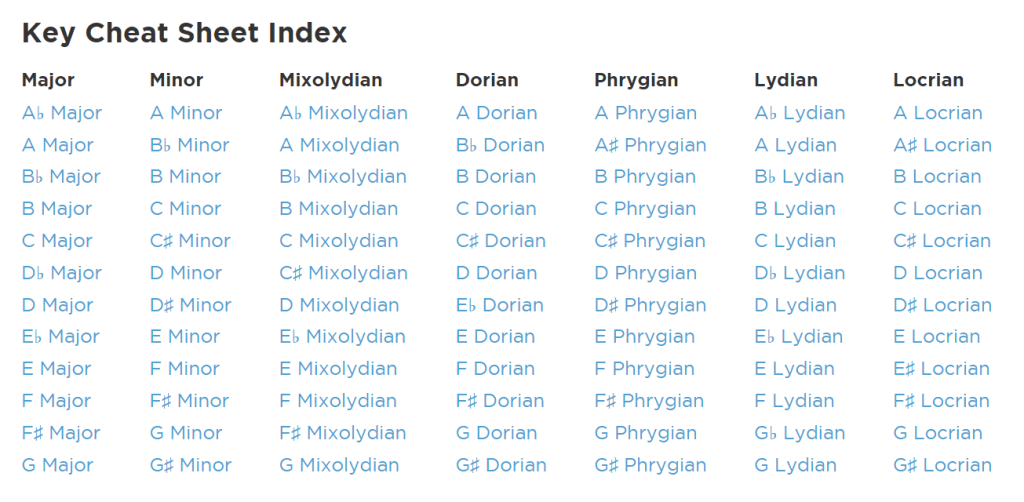
//https://www.hooktheory.com/cheat-sheet/key/g/phrygian
maxform1.Showmidiform(self);

This tune is from a G Phrygian and the key of G Phrygian has a key signature of 3 flats (B♭, E♭, and A♭).  In our notation its a sharp so A♭ is a g#.

PlayTune is a procedure which calls the midi device and controller in the following way:

procedure PlayTune(tune: array of string;pause: integer;octave: byte;fin: boolean;fmidi: IJclMidiOut);
var i, anote: integer;
begin
  for i:= 0 to High(tune) do begin
     anote:= StrtoMIDINote2(tune[i],octave);
     fmidi.SendNoteOn(2, anote, $7f); 
     delay(pause)  
     fmidi.SendNoteOff(2, anote, $7f); 
  end;
  if fin then sleep(1500);  
end;

We send note on and off messages in a sequence and we pass the device as fmidi. Noteon (i-rate note on) and noteoff (i-rate note off) are the simplest MIDI OUT opcodes. noteon sends a MIDI noteon message to MIDI OUT port, and noteoff sends a noteoff message. A noteon opcode must always be followed by an noteoff with the same channel and number inside the same instrument, otherwise the note will play endlessly. So we can also change the instrument in passing a midi channel and the instrument id:

MIDIMsgProgramChange = $C0;
fmidiout.SendProgramChange(2, 7);  //channel 2, instrument 7

To get a midi note we call the function StrtoMIDINote2(tune[i],octave);
function StrtoMIDINote2(Notestr: string; octave: byte): TMIDINote;

This conv.implementation assumes that the input string is in the format ‘NoteOctave’ (e.g., ‘C4’, ‘F#3’, ‘B5’,A4). 
It handles both sharp notes (with ‘#’) and natural notes but not flats one. If an invalid note is provided, the function returns -1.

It converts a string representation of a musical note to its corresponding MIDI note number. Here’s an implementation:  This function does the following:

  • It defines a constant array of note names.
    mnotes:= [‘C’,’C#’,’D’,’D#’,’E’,’F’,’F#’,’G’,’G#’,’A’,’A#’,’B’];
  • It extracts the note name and octave from the input string.
    NoteName := AnsiUpperCase(Copy(NoteStr, 1, Length(NoteStr) – 1));  
    Octave := StrToIntDef(Copy(NoteStr, Length(NoteStr), 1), 4);
  • It finds the index of the note in the Notes mnotes array by looping.
for I:= 0 to High(mNotes) do 
   if mNotes[I] = NoteName then begin
     NoteIndex:= I;
     write(mnotes[i]+' ')
     Break;
   end;

It calculates the MIDI note number using the formula: (Octave + 1) * 12 + NoteIndex.

https://studio.moises.ai/library/

Chord Progression

We can also play a chord progression. A chord progression is a sequence of two or more chords played one after the other. This is the chord:

https://www.hooktheory.com/cheat-sheet/key/g/phrygian

   for it:= 1 to 3 do begin

    playChord([‘g2′,’a#3′,’d4′,’g4’], 1100, false, fmidiout);   //gm

    playChord([‘c3′,’c4′,’d#4′,’g4’], 1100, false, fmidiout);  //cm

    playChord([‘a#2′,’a#3′,’d4′,’f4’], 1000, false, fmidiout); //bflat

    playChord([‘g#2′,’c4′,’d#4′,’g#4’], 900, true, fmidiout); //aflat 

   end; //}

https://www.hooktheory.com/cheat-sheet/key/g/phrygian

http://www.softwareschule.ch/examples/1321_KCP_Phrygian_4.mid

A cool function is the MIDI Note Frequency:

const
  HalftonesPerOctave = 12;
  MiddleA            = 440.0; // Hertz
  MidiMiddleA        = 69;    // A4 = 440 Hertz

function MIDINote(Hertz: Extended): Extended;
begin
  if Hertz < 1.0 then
    result:= mininteger  //Low(Integer)
  else
    result:= LogBase2(Hertz/MiddleA)*HalftonesPerOctave+MidiMiddleA;
end;

See also: https://www.colincrawley.com/midi-note-to-audio-frequency-calculator/

The Windows implememtation of the IJclWinMidiOut interface (not to confuse with the MIDI hardware interface) defines also stereo channels (not to confuse with a midi channel) with volume controls by both sides:

type
  TStereoChannel = (scLeft, scRight);
  
  // MIDI Out Definition
  IJclWinMidiOut = interface(IJclMidiOut)
    ['{F3FCE71C-B924-462C-BA0D-8C2DC118DADB}']
    // property access methods
    function GetChannelVolume(Channel: TStereoChannel): Word;
    procedure SetChannelVolume(Channel: TStereoChannel; const Value: Word);
    function GetVolume: Word;
    procedure SetVolume(const Value: Word);
    // properties
    property ChannelVolume[Channel: TStereoChannel]: Word read GetChannelVolume write SetChannelVolume;
    property Volume: Word read GetVolume write SetVolume;
  end;

Source of the script: http://www.softwareschule.ch/examples/midi3.htm

Source of the song: http://www.softwareschule.ch/download/zeitraum.mp3

modes of major scale

Code the Circle of Fifth

In music theory, the circle of fifths (sometimes also cycle of fifths) is a way of organizing pitches as a sequence of perfect fifths. Starting on a C, and using the standard system of tuning for Western music (12-tone equal temperament).

So we always start with C-Major and add an note-offset of 7 (a quint):

//g - a - h ^ c - d - e - fis ^ g  G-Dur
playTune2(['c4','d4','e4','f4','g4','a4','b4','c5'],300,7,true,fmidiout);
//d - e - fis ^ g - a - h - cis ^ d   D-Dur
playTune2(['c4','d4','e4','f4','g4','a4','b4','c5'],300,14,true,fmidiout);
//a - h - cis ^ d - e - fis - gis ^ a  A-Dur
PlayTune2(['c4','d4','e4','f4','g4','a4','b4','c5'],300,21,true,fmidiout);
//e - fis - gis ^ a - h - cis - dis ^ e  E-Dur
//https://de.wikipedia.org/wiki/E-Dur
playTune2(['c4','d4','e4','f4','g4','a4','b4','c5'],300,28,true,fmidiout);
https://de.wikipedia.org/wiki/C-Dur

And the result will be:

G4(67) A4(69) B4(71) C5(72) D5(74) E5(76) F#5(78) G5(79)

D5(74) E5(76) F#5(78) G5(79) A5(81) B5(83) C#6(85) D6(86)

A5(81) B5(83) C#6(85) D6(86) E6(88) F#6(90) G#6(92) A6(93)

E6(88) F#6(90) G#6(92) A6(93) B6(95) C#7(97) D#7(99) E7(100)

mX5🐞 executed: 18/11/2024 11:58:14 Runtime: 0:0:19.81 Memload: 69% use

Script: http://www.softwareschule.ch/examples/midi4.txt

The code is straight and based on conversions with StrtoMIDINote3(tune[i], offset); to set the offset and octave. This conversion as an array of string implementation assumes that the input string is in the format ‘NoteOctave’ (e.g., ‘C4’, ‘F#3’, ‘B5’,A4) and calls a function StrtoMIDINote3 within the procedure PlayTune2():

function StrtoMIDINote3(Notestr: string; offset: byte): TMIDINote;
var i: integer;
    NoteName: string;
    Octave, NoteIndex: Integer;  note:TMidinote;
begin
  mnotes:=['C','C#','D','D#','E','F','F#','G','G#','A','A#','B']; //+
  NoteName:= AnsiUpperCase(Copy(NoteStr,1, Length(NoteStr)- 1));
  Octave:= StrToIntDef(Copy(NoteStr,Length(NoteStr), 1), 4);
  // Find note index
  NoteIndex:= -1;
  for I:= 0 to High(mNotes) do 
    if mNotes[I] = NoteName then begin
      NoteIndex:= I+offset;
      Break;
    end;
  // Calculate MIDI note number & display
  if NoteIndex <> -1 then begin
    Result:= (Octave+1)*12 + NoteIndex
    write(midiNotetostr(result+12)+'('+itoa(result)+')'+' ');
  end else
    Result:= -1; // Invalid note 
end;

procedure PlayTune2(tune: array of string; pause,offset: integer; fin:boolean; fmidi: IJclMidiOut);
var i, anote: integer;
begin
  for i:= 0 to High(tune) do begin
     anote:= StrtoMIDINote3(tune[i], offset);
     fmidi.SendNoteOn(2, anote, $7f); 
     delay(pause)  
     fmidi.SendNoteOff(2, anote, $7f); 
  end;
  if fin then sleep(1500);  
  writeln(CRLF);
end;
https://de.wikipedia.org/wiki/C-Dur
ModeTonic relative
to major scale		Interval sequenceExample
IonianIW–W–H–W–W–W–HC–D–E–F–G–A–B–C
DorianiiW–H–W–W–W–H–WD–E–F–G–A–B–C–D
PhrygianiiiH–W–W–W–H–W–WE–F–G–A–B–C–D–E
LydianIVW–W–W–H–W–W–HF–G–A–B–C–D–E–F
MixolydianVW–W–H–W–W–H–WG–A–B–C–D–E–F–G
AeolianviW–H–W–W–H–W–WA–B–C–D–E–F–G–A
LocrianviiøH–W–W–H–W–W–WB–C–D–E–F–G–A–B

For the sake of simplicity, the examples shown above are formed by natural notes (also called “white notes”, as they can be played using the white keys of a piano keyboard). However, any transposition of each of these scales is a valid example of the corresponding mode.

https://flypaper.soundfly.com/write/scale-mode-cheat-sheet-how-to-remember-each-and-every-mode/
https://www.hooktheory.com/cheat-sheet/key/c/minor
5 Nation Locomotion
Pip Install
Short History of Industrial Design
BPM #120
See the difference

Published by maxbox4

Code till the End

2 thoughts on “MIDI Magic”

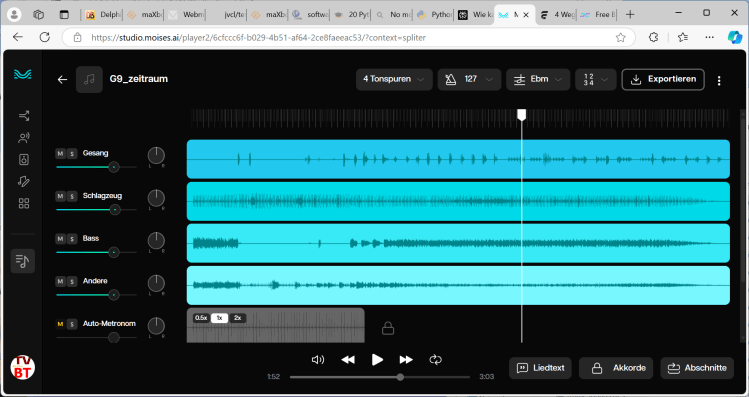
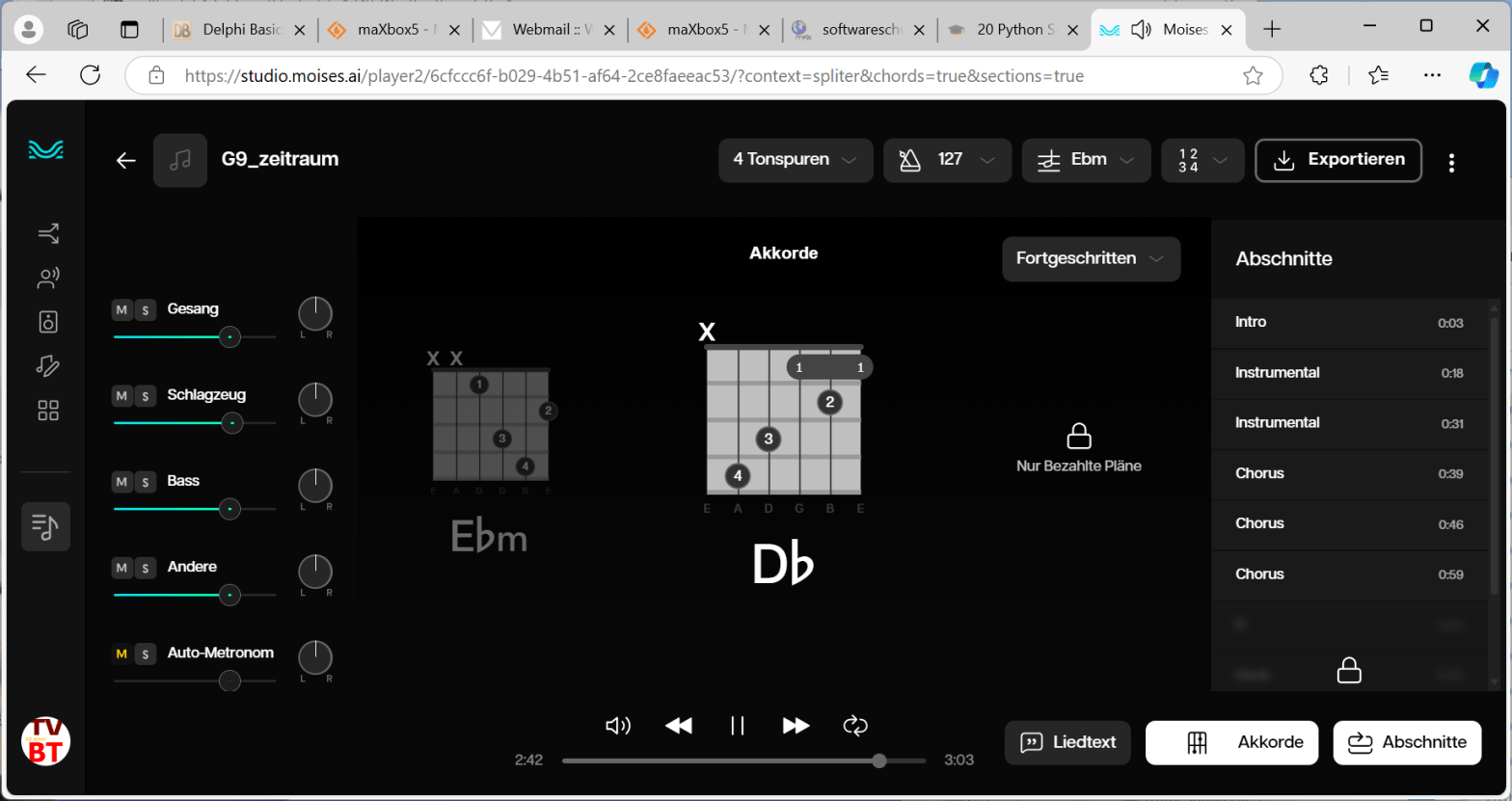
  2. Moises is an innovative AI-powered music application designed to enhance the practice and creative processes of musicians at all levels. The app offers a suite of features including AI audio separation, which allows users to isolate or remove specific instruments and vocals from songs.

    Like

    Reply

Leave a comment

Design a site like this with WordPress.com
Get started